Intro to Computer Engineering

Assignment 1 - Finite State Binary Counter

Access your repository

Click here to access the Canvas page with the repository for this assignment.

The idea

This assignment contains two parts: binary puzzles and a binary counter. In this assignment you will: a) use bitwise and Boolean operators to solve basic logical operations on numbers and b) use finite-state machines to model a binary counter. These logic puzzles will help you better understand how binary fits into the day-to-day mechanics of computing. In other words, this assignment will help you think about how computers actually look at and understand data that they interact with.

Objectives

By the end of this assignment, you should know:

Part I Binary Puzzles

• how to use bitwise and Boolean operators
• when to use specific numerical Arduino data types
• how to read function signatures
• how to structure Arduino code
• how to automate the build process

Part II Binary Counter

• FSMs
  • How to make them
  • When to use them
  • How they can help a program’s clarity and design
• What an enum is and how it is helpful to a programmer
• how to print to the Serial Monitor
• how to call functions in Arduino C
• how to count to 7 in Binary
• how to use delay()

The background

Bitwise and Boolean operators

It’s hard to talk about numbers at all without talking about operators. You should be familiar with many of them already: +, -, *, etc. They take one or two numbers and operate on them, changing them. We introduce two new groups of operators: bitwise operators and Booleans ones.

Bitwise operators are operators that act directly on the individual bits of a binary number, whereas Boolean operators (also known as logical operators) operate on the “logical values” that the complete number represents: in Arduino, 0 is a logical false, and anything else is true (even -1).

In a sense, these two groups of operators are very closely related: both operate only on two values (Boolean operators treat everything as either true or false, and bitwise operators operate on the underlying bits of numbers which can each only be 0 or 1), and as you’ll see in a bit, they perform very similar operations on these values. Their main difference is their scope: bitwise operations work on each bit individually, whereas Boolean operations work on the numbers as a whole.

The operations proper

• Bitwise AND (c = a & b), c has 1s in the places where both of the corresponding bits in a and b are 1.
• Bitwise OR (c = a | b), c has 1s wherever at least one of the corresponding bits in a and b is 1.
• Bitwise XOR (c = a ^ b), c has 1s wherever one and only one of the corresponding bits in a and b is 1.
• Bitwise NOT (c = ~a), c is a with each bit inverted.
• Right shift (c = a >> b), c is a, with each bit moved lower b places.
• Left shift (c = a << b), c is a, with each bit moved higher b places.
• Boolean AND (c = a && b), c is 1 if both a and b are non-zero.
• Boolean OR (c = a || b), c is 1 if either a and b are non-zero.
• Boolean NOT (c = !a), c is 1 only if a is 0.

Characters, integers, & longs

Not all numbers are the same length. Because of this it is useful to have several different data types that we can choose from for storing differently sized numbers. In this way we don’t waste space storing small numbers in large spaces. The three data types we will use in this lab are characters (char: 1 byte), integers (int: 2 bytes), and longs (long: 4 bytes), each of which store whole numbers.

By default, all of these values are signed and can store both positive and negative numbers. Their possible values range from and , where n is the number of bits in the data type. unsigned numbers range from 0 to . e.g. unsigned char, unsigned int and unsigned long.

Two’s complement is used here to store signed numbers. If you still have confusions about signed and unsigned numbers, please read Introduction to Information Representation guide for detailed explanations.

• Characters (char) : Smallest addressable unit that can contain integer data. They are 1 byte (8 bits) in length. Signed characters range between -128 and +127.
• Integers (int) : Standard unit to contain integer data. In Arduino C, they contain 2 bytes—16 bits. Signed integers range between -32,768 and 32,767.
• Longs (long or long int) : In Arduino C, they contain 4 bytes or 32 bits. Signed longs range between -2,147,483,648 and 2,147,483,647.

Note: Data types in Java or traditional C have different lengths than in Arduino C.

The Assignment

Part I Binary Puzzles

Open the Arduino sketch called binaryPuzzles.

1. Bit shifting!

   Complete the functions shiftRight and shiftLeft.

   • unsigned shiftRight(unsigned num, int n): Shift num to the right n bits.
   • int shiftLeft(int num, int n): Shift num to the left n bits.

2. Bit manipulations!

   For each function below, use only the bitwise and Boolean operators listed above (i.e., no if-then tests, comparisons (e.g., ==, !=, >, <, >=, <=), arithmetic operators (e.g., *, +, -, /, %) or for/while loops are allowed) to write functions that return 1 if the input matches the condition given and 0 otherwise. You may use constant values (e.g., 0, 1, 255, etc.) in your operations. You should be able to solve each in one line.

   • int hasAOne(int num): At least one bit in num is a one (Binary Representation).
     E.g. 7 is 111 in base 2. Therefore hasAOne(7) should return 1(true).
   • int hasAZero(int num): At least one bit in num is a zero.
   • int leastSigByteHasAOne(int num): At least one bit in the least significant byte(the last byte) of num is a one. (This is NOT just testing whether the lest significant bit is a one.
   • int isNegativeInt(int num): the integer num is negative.
     Hint: We use Two’s complement to represent signed numbers.
   • int isNegativeLong(long num): the long num is negative. Remember, in Arduino C longs are 4 bytes (32 bits) in length.
   • int isNegativeChar(char num): the char num is negative. Remember, in Arduino C chars are 1 byte (8 bits) in length.
   • int negate(int num): Return the two’s complement negation of num. This function should return a number instead of 1 or 0 (true or false).
     Exception: You are allowed to use the + operator for this one (not allowed for the functions above).

Part II Binary Counter

This part has two components: drawing a FSM, and modeling said FSM on your Arduino.

Setup

• Connect your Arduino
• Open FSM / FSM.ino

The Model

The Studio has useful information for this lab. If you were unable to finish the studio last class we recommend you look it over before starting on the assignment.

Interpreting FSMs and FSAs

Here is the drawing of the Studio 1 FSM:

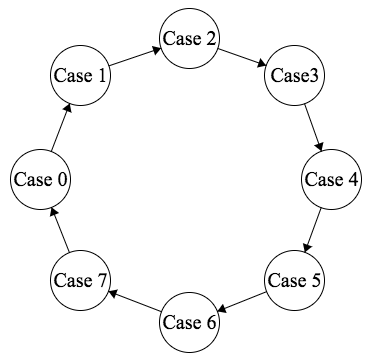
• The circles represent the possible states the machine can be in, and each circle has its own set of instructions.
• The arrows represent the possible movements the machine can make.
• Notice that this FSM has no inputs. It continuously progresses from one state to the next. This is about to change!

For more information on how to create effective FSMs, watch a short video here.

Drawing Your Model

• Draw a FSM to model a Binary Counter that can reverse directions
  • You are welcome to turn in a picture of one drawn by hand, but we recommend this Finite State Machine Designer. This program allows you add, move, and delete states more freely than pen and paper.
  • Save the PNG or other image format to your repository in the FSM directory.
  • We want to use an input to dictate when we should reverse directions. For this lab, our input will come from the keyboard. In your FSM however, you could represent the input as a binary value: 1 if a key has been pressed, and 0 if not.
  • Hint – your model should have 16 states One set of states is for counting up and another set for counting down. If you were to only use 8 states to represent the current number, how would the FSM know whether it should count up or down? We would need another variable to keep track of which way we are counting (which effectively adds additional states to the FSM in a rather crude and unsophisticated way).

The Program

Transferring FSMs to Code

• Return to FSM.ino
• Complete the function determineNextState() with a FSM to determine the next state of the machine.
  • Using your FSM drawing as a guide, your FSM should have 16 states and a matching enum.

Here is an Example of an Enum in Arduino C:

enum Direction {
  	 North,			// North = 0
  	 East,			// East = 1
  	 South,			// South = 2
  	 West			// West = 3
} direction = North;

• Recommended – use switch statements to switch between your states using cases
  • Correctly designed if statements will also be accepted

Here is some pseudocode to demonstrate switch:

month = 2
switch (month) {
	case 1:
		print 'January'
		break
	case 2:  		// switch to case 2 because month == 2
		print 'February' 	
		break		// break so other cases won't run
	case 3:
		print 'March'
		break
	... 
}

Adding the Reverse Button

• Complete the function checkReverse() , which reverses the direction of the counter if a key on the keyboard has been pressed.
  • To check if a key on the keyboard has been pressed, you can use Serial.read(). Take a look at the documentation to see how this function works, then use it to complete this method.
  • For this lab, we don’t care which key has been pressed, we only care about whether or not any key has been pressed.
  • If the user has input something, checkReverse() should update the state to reflect this. (Be sure the serial monitor has No line ending selected. Other options, like Newline will send one or more additional characters and may cause it to reverse multiple times.)**

The Final product

Your Output should look close to this:

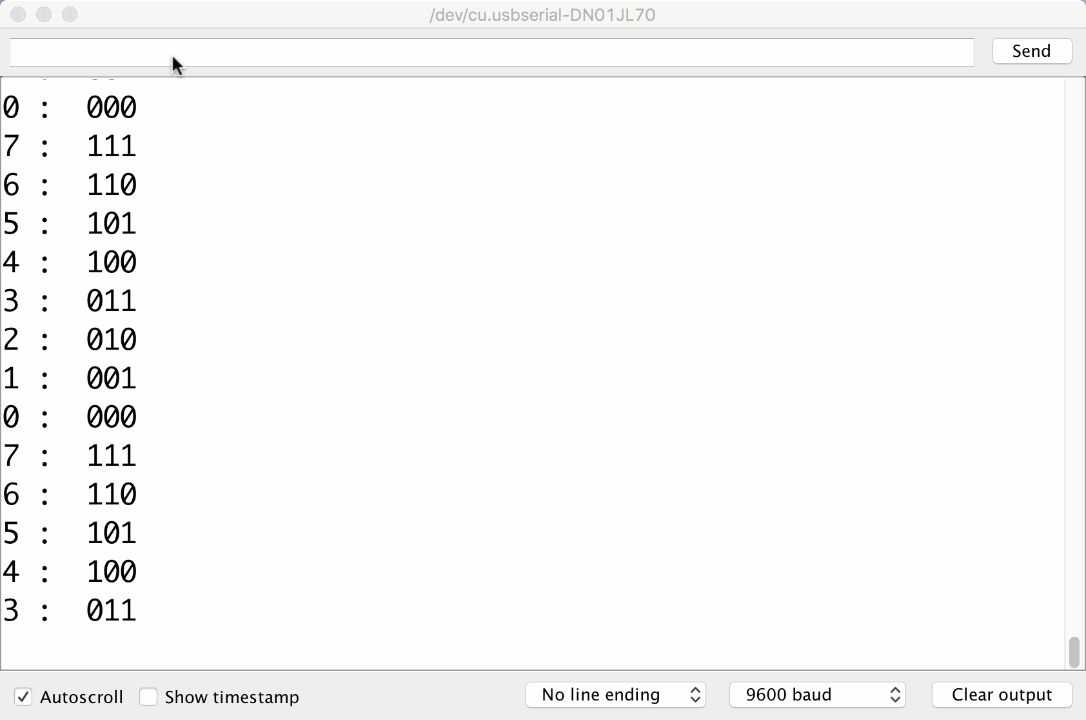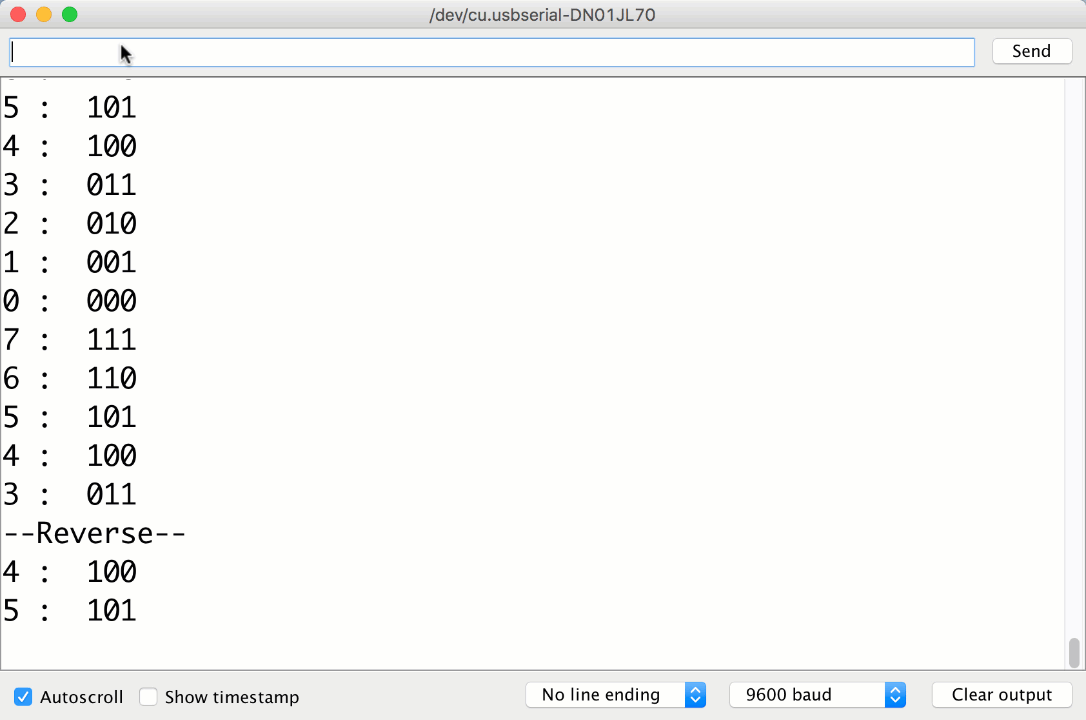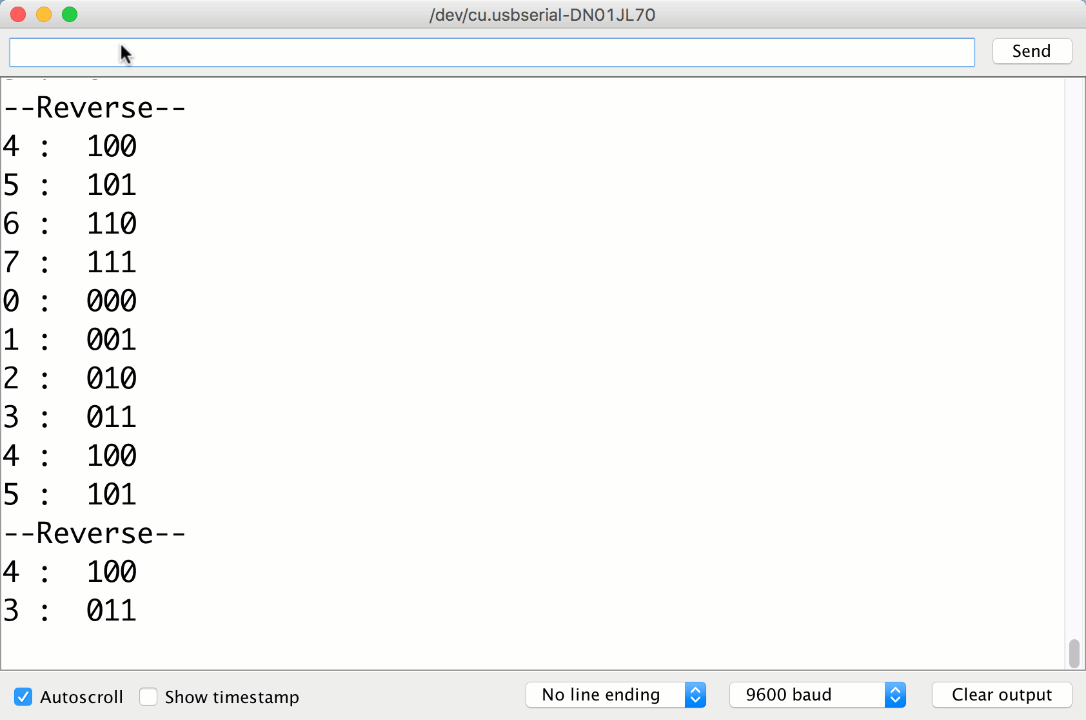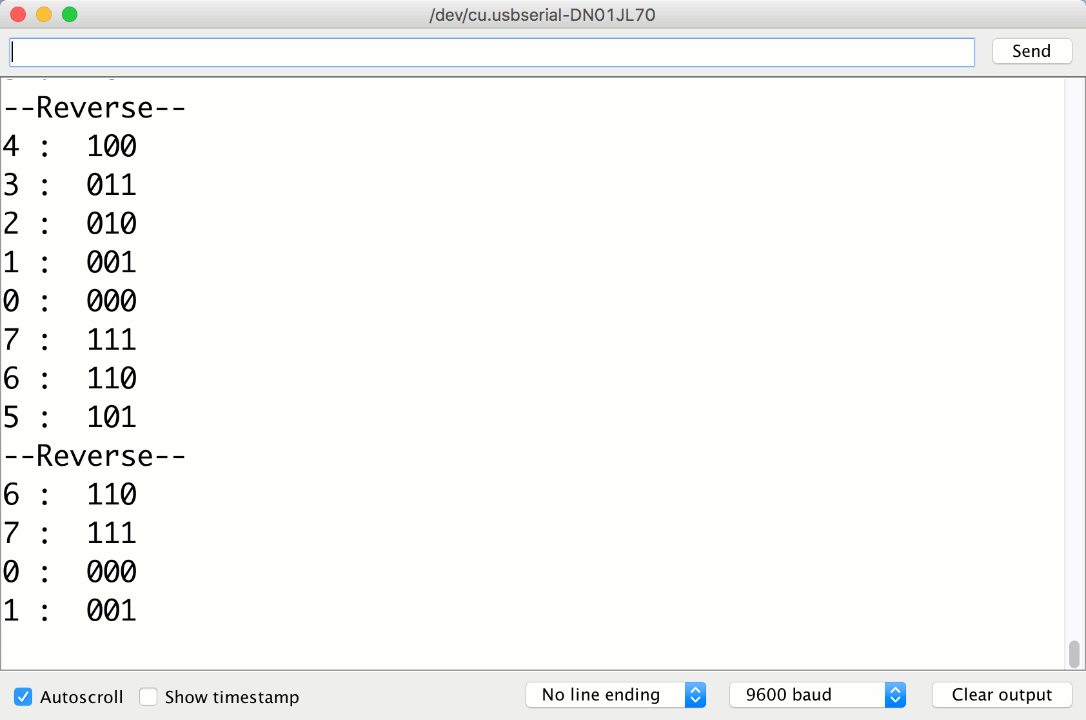
We also accept reversing after the next state change, as shown in this older video. Note that it also showed state bits in the incorrect order (least significant bit leftmost rather than rightmost).

The check-in

1. Commit and push your code (and FSM), then verify in GitHub that it is all there.
2. Follow the checklist below to see if you have everything done before demoing your assignment to a TA.
   • Part I Binary Puzzles
     • All functions work correctly and only contain the approved operators (45 points)
       • shiftRight(int num, int n)
       • shiftLeft(int num, int n)
       • hasAOne(int num)
       • hasAZero(int num)
       • leastSigHasAOne(int num)
       • isNegativeInt(int num)
       • isNegativeLong(long num)
       • isNegativeChar(char num)
       • negate(int num)
   • Part II Binary Counter
     • Drawn FSM (20 points)
       • 16 states
       • correctly models the counter
     • FSM (30 points)
       • determineNextState() filled out and working
       • 16 states
       • uses enums
       • switches from state to state with switch or if statements
       • working counter printed out in the Serial Monitor
     • Reverse Button / Lever (5 points)
       • can switch the direction of the counter
   • All of your files are committed
3. Assignment Demo
   

0  :  000
1  :  001
2  :  010
3  :  011
4  :  100
--Reverse--
3  :  011
2  :  010
1  :  001
--Reverse--
2  :  010
3  :  011
--Reverse--
2  :  010
1  :  001
0  :  000
7  :  111
6  :  110
5  :  101
--Reverse--
6  :  110
7  :  111
0  :  000
--Reverse--
7  :  111
6  :  110
5  :  101
4  :  100

1. Check out with a TA.

Generated at 2025-10-30 17:49:09 +0000.
Page written by Sean Schaffer, Claire Heuckeroth, Ben Stolovitz and Shuya Ma.